人工衛星が地球の周りを回転するときの惑星等の重力と人工衛星の速さ、軌道半径等の関係を体感する実験です。
○こんなことが学べます
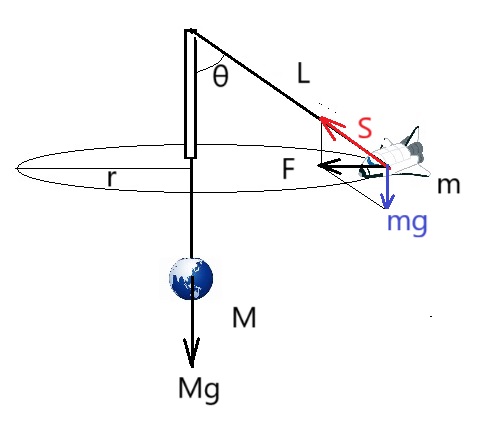
実験の配置図を下に示します。
等速円運動を行っているとき、糸の張力Sは地球からの重力Mgに等しくなります。
人工衛星が回転するための向心力Fは、張力Sと人工衛星の重力mgとの合力になります。
人工衛星の速さをvとすると
S=Mg、Scosθ=mg ∴m=Mcosθ
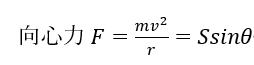 より、
より、回転の周期Tは、
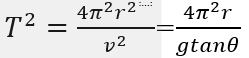
より、周期Tの二乗は、半径rに比例する。

3Dプリンタで作った地球とスペースシャトル等の地球を周回する衛星の模型、ボールペンの軸やガラス管(両端を滑らかにする)、糸1m程度
○作ってみよう
① 両端が滑らかなボールペンの管等に糸を通す。
② 3Dプリンタで作った地球やスペースシャトル等を糸の両端に取り付ける。
地球やスペースシャトル等に色を塗ると良い。

管を持って人工衛星を等速円運動させ、地球のおもりと釣り合って、糸の長さ(回転半径)が一定になるようにする。
人工衛星を速く回転させると、回転半径が大きくなる。
腕による回転を止めると、回転半径が小さくなり、人工衛星は次第に速くなって管に当たる。これは地球への落下に相当する。
地球のおもりを重くすると、同じ回転半径だと人工衛星の回転速度を大きくしないといけない。
参考:啓林館「総合物理1」p.161
実験方法
あらかじめ決められた回数(10回とか)回転した時間を測る。このとき、糸の長さが一定になるように糸に目印を付ける。
① 人工衛星と地球を変えずに、回転の半径を変える。
② 人工衛星と回転半径を一定にして、おもりの地球の質量を変える。
③ 地球と回転半径を一定にして、人工衛星の質量を変える。
処理
① T^2とrの関係をグラフにする。
② T^(-2)とS(=Mg)との関係をグラフにする。
③ T^2とmの関係をグラフにする。