| �����̗�܂����i2007�N���{�Z���^�[�e�X�g�����@��S�̂b�j�̎����Ɛ����ɂ���@ | |
| �M�≷�x�ɂ��Đ������������Ă��Ȃ��Ɖł��Ȃ���肪�o�肳�ꂽ�B�Z�p�ɂ͂Ȃ��ǖ�ł���B���ۂǂ��Ȃ�̂��������C�܂��C��ʓI�Ȓl�Ɣ�r���邽�߁C�����ɂ���@�����߂Ă݂��B |  |
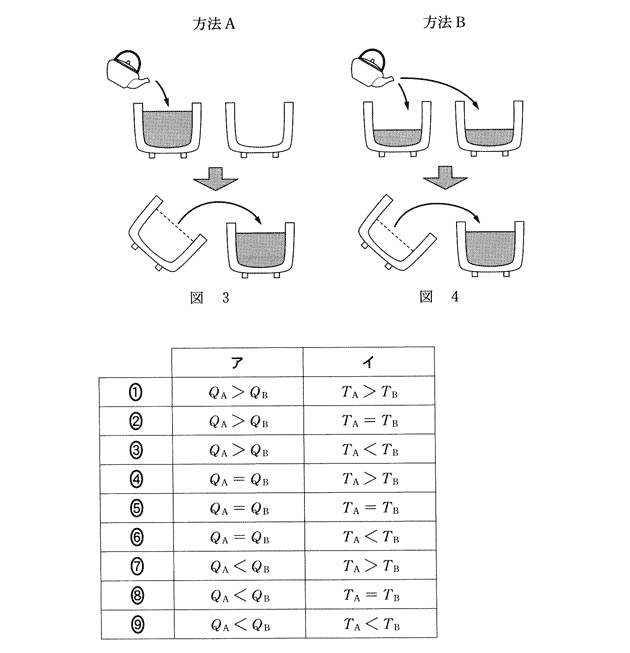
| �y���ʁz ���߂̓��̉��x�@�U�U���@�����@�Q�P�� ��V�̕��@�ł�����Е��̒��q�ֈڂ��C�P����Ɍ��̒��q�ֈڂ��đ���B �@�߂�������@A�̕��@�F�@�S�R�� �@�@�@�@�@�@�@�@ �a�̕��@�F�@�S�U���@�@ ���̌�P�����ɑ��肵�����C�R���̍��̂܂܂P�T���ԉ��x�͉������Ă������B |
|
 |
|
 |
|
| �y��@�z ���@�`�C�a�ŗp����e�����݂̔M�e�ʂ��b���C���̔M�e�ʂ��b���C�ŏ��̓����݂̉��x�i�����ɓ������j���������ɍ��킹�Ăs1�C�ŏ��̂����̉��x���s0�Ƃ���B �P�@���@A �ŏ��̑���ŁC�P�߂̓����݂Ƃ����̉��x���sa1�ɂȂ����Ƃ���ƁC�P�ڂ̓����݂�������M�ʂpca1�́C �@�@�pca1���b���i�sa1�|�s1�j �������������������M�ʂpwa1�́C �@�@�pwa1���b���i�s0-�sa1�j �M�ʕۑ��̖@�����pca1���pwa1�ƂȂ邽�߁C �@�@�sa1���i�bw�s0�{�bc�s1�j/�i�bw�{�bc�j ���������āC�P�ڂ̓����݂�������M�ʂpA�́C �@�@�pA���pca1���bc�i�i�bw�s0�{�bc�s1�j/�i�bw�{�bc�j�|�s1�j �@�@�@�@ ���bw�bc�i�s0-�s1�j/�i�bw�{�bc�j �ƂȂ�B ���ɁC���̂������Q�ڂ̓����݂Ɉڂ����Ƃ��C�����݂Ƃ����̉��x���sa2�ɂȂ����Ƃ���ƁC�Q�ڂ̓����݂̎�����M�ʂpca2�́C �@�@�pca2���b���i�sa2�|�s1�j �������������������M�ʂpwa2�́C �@�@�pwa2���b���i�sa1-�sa2�j �M�ʕۑ��̖@�����pca2���pwa2�ƂȂ邽�߁C �@�@�sa2���i�bw�sa1�{�bc�s1�j/�i�bw�{�bc�j �@�@�@�@���i�b��2�s0�{�Q�bw�bc�s1�{�bc2�s1)/�i�bw�{�bc�j2 ���ꂪ�sA�ł���B �Q�@���@�a �Q�̓����݂͓����ɓ������x�̂������ʒ������߁C�������x�ɂȂ�B���߂ɂ������������Ƃ��̓����݂Ƃ����̉��x���sb1�ɂȂ����Ƃ���ƁC�P�̓����݂̎�����M�ʂpcb1�́C �@�@�pcb1���b���i�sb1�|�s1�j �������������������M�ʂpwb1�́C���@�`�̔����̗ʂ̂����𒍂����߁C���i�����j�̔M�e�ʂ������̂b��/2�ɂȂ�C �@�@�pwb1���b��/2�i�s0-�sb1�j �M�ʕۑ��̖@�����pcb1���pwb1�ƂȂ邽�߁C �@�@�sb1���i�bw�s0�{�Q�bc�s1�j/�i�bw�{�Q�bc�j ���ɁC���̂������Q�ڂ̓����݂Ɉڂ����Ƃ��C�Q�ڂ̓����݂́C�P�ڂƓ��������łł�����������Ă��邽�߁C�����̉��x�͂P�ڂƓ����܂܂̂sb1�ł���B���ꂪ�s�a�ł���B �@ ��ɂȂ��������݂��������M�ʂpB�́C�P�ڂ̓����݂�������M�ʂpcb1�Ȃ̂ŁC �@�@�p�a���b���bc�i�s0-�s1�j/�i�bw�{�Q�bc�j �ƂȂ�B ���������āC �@�@�@�pA�|�p�a���bw�bc2�i�s0-�s1�j/�i�i�bw�{�bc�j�i�bw�{�Q�bc�j�j���O�@ �@���@�pA���p�a �@��s0�͍ŏ��ɉ��M���������̉��x�ł���C�s1�͎���������B �@ �@�@�@�s�a�|�sA���bw�bc2�i�s0-�s1�j/�i�i�bw�{�bc�j2�i�bw�{�Q�bc�j�j���O�@�@�@���@�s�a���sA �@ ���������̂͑I�����̇B�ł���B ���Ȃ݂�Cw��Cc�̔��͐��Ɠ����݂̔M�e�ʂ̔�ł���C���ʂ������Ƃ��͖��S�D�Q�F�O�D�X�ł���B�܂��C�s0���U�U���C�s1���Q�P���̒l�Ōv�Z����ƁC �@�@�sA���S�V���C�s�a���T�Q�� �ƂȂ邪�C���ۂ͎��͂֔M�������Ă������߁C�����̉��x��菬���Ȓl�ɂȂ�B�@�@ |
|
 |
|
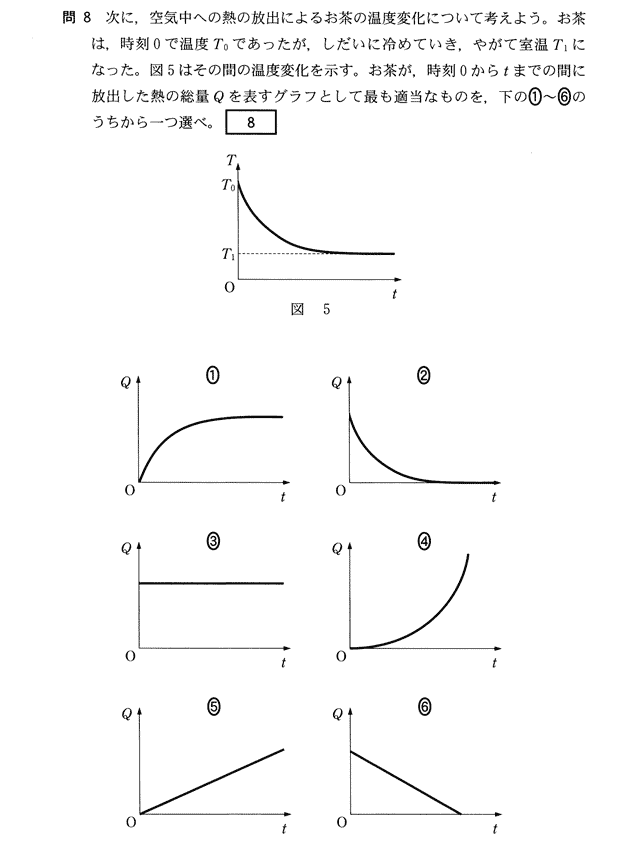
| �y��@�z ��p�Ȑ��͐}�T�̂悤�ɉ��x���w�����I�Ɍ������邽�߁C�ŏ����x�̒l���傫���������Ă���Ƃ��́C��ʂɓ����݂��C���ɔM���ړ����邪�C�����ɋ߂Â��ɂ�C�M�̈ړ��͓݉����C�O���t�͂�����l�ɂȂ�B���̂��ߓ��͇@�ɂȂ�B �ł́C���o���Ă݂悤�B �u����ʁi�����ł͎����Ƃ̉��x���s-�s1���s�f�j�̕ω��̑����i�����ʂ̎��ԕω��j�����̗͂ʂɔ�Ⴗ��v�Ƃ����j���[�g���̎����C���萔���ɂƂ��āC �@�@-���s�f/�������ɂs�f ���̎��͕ϐ������`�ɂ��Đϕ�����Ƃ悢�B �@�@���s�f/�s�f��-�ɂ����@�@�@�@�@�炄�s�f/�s�f��-�Ɂ炄���@�@�@���@ln�s�f��-�ɂ��{�b�@�@�s�f��e-�ɂ��{�b��e-�ɂ�e�b �����O�łs���s0�Ƃ���ƁC�@�s0-�s1��e�b ���������āC�}�T�̃O���t�̎����ȉ��̂悤�ɓ�����B �@�@�s���i�s0-�s1�je-�ɂ��{�s1 ���ɂ�������C���֕��o�����M�ʂ��l����B���߂̏����u�����݈ȊO�ւ̔M�̗��o�͂Ȃ����̂Ƃ���v�Ƃ͈ꌩ�������邪�C���̏����͂����z�����u�ԂƑ����邵���Ȃ��B���ԂƂƂ��ɔM�͂����̐��ʂƓ����݂̕\�ʂ�ʂ��ċ�C���֓����Ă����B |
|
| ���͂֎��ԂƂƂ��ɂ������瓦���Ă����M�ʂp�i���j�́C�����̎������M�ʂȂ̂ŁC �@�@�p�i���j���bw���s���bw�i�s0-�s�j�@�@��@�����͉��x�s0���炾�����Ă������߁C�����̉��x�ω����s�͂��̂悤�ɂȂ�B �@���@�p�i���j���bw�i�s0-�s1-�i�s0-�s1�je-�ɂ��j �ƂȂ�B����͇@�̃O���t�ɂȂ�B�@ |
|